Post

子序列问题

Posted
By Ahern
19 min read
子序列问题

子序列问题思路总结

思路 1：一维 dp 数组

1
2
3
4
5
6
7
8
9
10
11
12

func dp(nums []int) int {
	// dp[i]表示以nums[i]结尾的最长递增子序列的长度， 包括nums[i]
	// note: 不是前i个元素的最长递增子序列的长度
	dp := make([]int, len(nums))	
	for i := 1; i <len(nums); i++ {
		for j := 0; j < i; j++ {
			if nums[i] > nums[j] {
				dp[i] = 最值(dp[i], dp[j]+1)
			}
		}
	}
}
  • dp[i]表示以nums[i]结尾的最长递增子序列的长度，因为需要用到 nums[i] 做比较
  • 如：最长递增子序列-300

思路 2：二维 dp 数组

1
2
3
4
5
6
7
8
9
10
11
12

func dp(nums1 []int, nums2 []int) int {
	for i := 1; i <= len(nums1); i++ {
		for j := 1; j <=len(nums2); j++ {
			if nums1[i-1]==nums2[j-1]{
				dp[i][j]=dp[i-1][j-1]+1
			}else{
				dp[i][j]=最值(dp[i-1][j],dp[i][j-1])
			}
		}
	}
	return dp[len(nums1)][len(nums2)] 
}
  • dp[i][j]表示nums1[0…i], nums2[0…j]最长公共子序列
  • 如：最长公共子序列-1143

最长连续递增序列-674

设dp[i]表示以nums[i]结尾的最长递增子序列的长度（包括nums[i]），且要求连续递增序列

Note: 最长连续递增子序列的长度不一定包含最后一个元素，所以需要一个变量记录最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

func findLengthOfLCIS(nums []int) int {
	if len(nums) <= 1 {
		return len(nums)
	}

	maxLength := 1
	dp := make([]int, len(nums)) // dp[i]表示以nums[i]结尾的最长连续递增子序列的长度
	dp[0] = 1 // 初始条件
	for i := 1; i < len(nums); i++ {
		if nums[i] > nums[i-1] {
			dp[i] = dp[i-1] + 1
		} else {
			// 初始条件
			dp[i] = 1
		}

		// 最长连续递增子序列的长度不一定包含最后一个元素，所以需要比较
		if dp[i] > maxLength {
			maxLength = dp[i]
		}
	}

	return maxLength
}

最长递增子序列-300

设dp[i]表示以nums[i]结尾的最长递增子序列的长度（包括nums[i]）

dp[i]不是前i个元素的最长递增子序列的长度, 为什么？

答：因为需要比较递增，如果dp[i]表示前i个元素的最长递增子序列的长度，并不知道最后一个元素是哪一个

要求 dp[i], 也就是找到最大的 dp[j]（0 <= j < i）且 nums[i] > nums[j]。

需要注意的是：并不是 dp 数组最后一个元素为最终结果，应该最大子序列不一定包含最后一个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

func lengthOfLIS(nums []int) int {
	// dp[i]表示以nums[i]结尾的最长递增子序列的长度， 包括nums[i]
	// note: 不是前i个元素的最长递增子序列的长度
	dp := make([]int, len(nums))
	for i := 0; i < len(nums); i++ {
		dp[i] = 1 // 初始化，每个元素本身就是一个递增子序列
	}
	
	maxLength := dp[0]
	for i := 1; i <len(nums); i++ {
		for j := 0; j < i; j++ {
			if nums[i] > nums[j] {
				dp[i] = max(dp[i], dp[j]+1)
			}
		}

		// 最长递增子序列的长度不一定包含最后一个元素，所以需要比较
		if dp[i] > maxLength {
			maxLength = dp[i]
		}
	}

	return maxLength
}

最长重复子数组-718

用指针 i 遍历数组 A，指针 j 遍历数组 B，当A[i] == B[j]时，说明存在公共子序列了，还需要看各自前一个元素的最长公共子序列（i-1、 j-1）。

设dp[i][j] 表示 A 数组以 i-1（不用纠结 i-1, 临界问题） 处结尾，B 数组以 j-1 处结尾的最长公共子序列长度。 当 A[i] == B[j] 时；此时出现公共子序列，到底有多少个呢？还得看看就要看各自前一个元素的最长公共子序列长度。 得出状态转移方程： \(dp[i][j] = dp[i-1][j-1] + 1\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// dp[i][j] 表示 A 数组以 i-1 处结尾，B 数组以 j-1 处结尾的最长公共子序列长度
	dp := make([][]int, len(nums1)+1)
	for i := range dp {
		dp[i] = make([]int, len(nums2)+1)
	}

	result := 0
	// 遍历数组 A
	for i := 1; i < len(nums1)+1; i++ {
		// 遍历数组 B
		for j := 1; j < len(nums2)+1; j++ {
			// 如何果两个元素相等，就要看各自前一个元素的最长公共子序列长度，加 1 即可
			if nums1[i-1] == nums2[j-1] {
				dp[i][j] = dp[i-1][j-1] + 1
			}

			// 最长公共子序列不一定在 dp[len(nums1)][len(nums2)]，需要随时记录最大值
			if dp[i][j] > result {
				result = dp[i][j]
			}
		}
	}

	return result

？最长公共子序列-1143

设 dp[i][j] 表示 text1 在 0～i 范围，text2 在 0～j 范围的最长公共子序列。

有两种情况： 1、当text1[i] == text2[j]；表明该字符属于公共子序列，则 dp[i][j] = dp[i-1][j-1] + 1。（不理解？？）
2、当text1[i] != text2[j]；最长公共子序列可能存在text1[i-1]、text2[j] 或 text1[i]、text2[j-1]中。则取 dp[i-1][j] 和 dp[i][j-1] 最大值

状态转移方程：

\[dp[i][j] = \begin{cases} dp[i-1][j-1] + 1, & \text{if } text1[i] == text2[j] \\[6pt] max(dp[i-1][j], dp[i][j-1]), & \text{if } text1[i] != text2[j] \\[6pt] \end{cases}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

func longestCommonSubsequence(text1 string, text2 string) int {
	t1 := len(text1)
	t2 := len(text2)
	dp:=make([][]int,t1+1)
	for i:=range dp{
		dp[i]=make([]int,t2+1)
	}

	for i := 1; i <= t1; i++ {
		for j := 1; j <=t2; j++ {
			if text1[i-1]==text2[j-1]{
				dp[i][j]=dp[i-1][j-1]+1
			}else{
				dp[i][j]=max(dp[i-1][j],dp[i][j-1])
			}
		}
	}
	return dp[t1][t2]
}

不相交的线-1035

nums1[i] == nums2[j] 就可以连线；且要求连线不能相交，在 nums1、nums2 中寻找相同字符的相对顺序一致，这样就不会相交。

所以这也是一道求最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

func maxUncrossedLines(nums1 []int, nums2 []int) int {
    dp := make([][]int, len(nums1) + 1)
    for i := range dp {
        dp[i] = make([]int, len(nums2) + 1)
    }

	for i := 1; i <= len(nums1); i++ {
		for j := 1; j <= len(nums2); j++ {
			if (nums1[i - 1] == nums2[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1
			} else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
			}
		}
	}
	
	return dp[len(nums1)][len(nums2)]
}

最大子序和-53

题目要点：求最大和的连续子数组。

设 dp[i] 表示以 nums[i] 结尾的最大连续子序列和。 在计算 dp[i] 时，就是需要考虑 nums[i] 是否需要与前面子序列拼接（dp[i-1]）,也就是：

1
2
3

if nums[i] + dp[i-1] > nums[i] {
	dp[i] = nums[i] + dp[i-1]
}

最大和的连续子数组不一定包括最后一个元素，所以需要一个变量记录最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

func maxSubArray(nums []int) int {
	if len(nums) == 0 {
		return 0
	}

	// dp[i] 表示以 nums[i] 结尾的最大连续子序列和
	dp := make([]int, len(nums))
	for i := 0; i < len(nums); i++ {
		// 初始化条件；不拼接之前的子序列
		dp[i] = nums[i]
	}

	result := dp[0]
	for i := 1; i < len(nums); i++ {
		// 考虑 nums[i] 是否需要与前面子序列拼接（dp[i-1]）
        if nums[i] + dp[i-1] > nums[i] {
			dp[i] = nums[i] + dp[i-1]
		} 

		// 记录最大结果
		if dp[i] > result {
			result = dp[i]
		}
	}

	return result
}

判断子序列-392

题意可以转化成：求s、t的相同子序列长度，并判断相同子序列的长度是否等于len(s)。

dp[i][j] 表示以s[i-1]、t[j-1]结尾的相同子序列长度。 遍历s和t，有两种情况：
1、如果s[i] == t[j], 与最长公共子序列一样
2、如果s[i] != t[j], 则需要剪掉t[j]字符，继续匹配，也就是：dp[i][j] = dp[i][j-1]

与最长公共子序列不同的是，并不再需要考虑剪掉s[i-1]（dp[i-1][j]）字符情况。因为s剪掉字符，不再符合题意。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

func isSubsequence(s string, t string) bool {
	// dp[i][j] 表示以s[i-1]、t[j-1]结尾的相同子序列长度
	dp := make([][]int, len(s)+1)
	for i := 0; i < len(s)+1; i++ {
		dp[i] = make([]int, len(t)+1)
	}

	for i := 1; i < len(s)+1; i++ { // 遍历子串
		for j := 1; j < len(t)+1; j++ { // 遍历原始字符串
			if s[i-1] == t[j-1] {
				dp[i][j] = dp[i-1][j-1] + 1
			}else {
				// 原始字符串 剪掉当前字符，等于前一个字符的结果
				dp[i][j] = dp[i][j-1] 
			}
		}
	}

	return dp[len(s)][len(t)] == len(s)
}

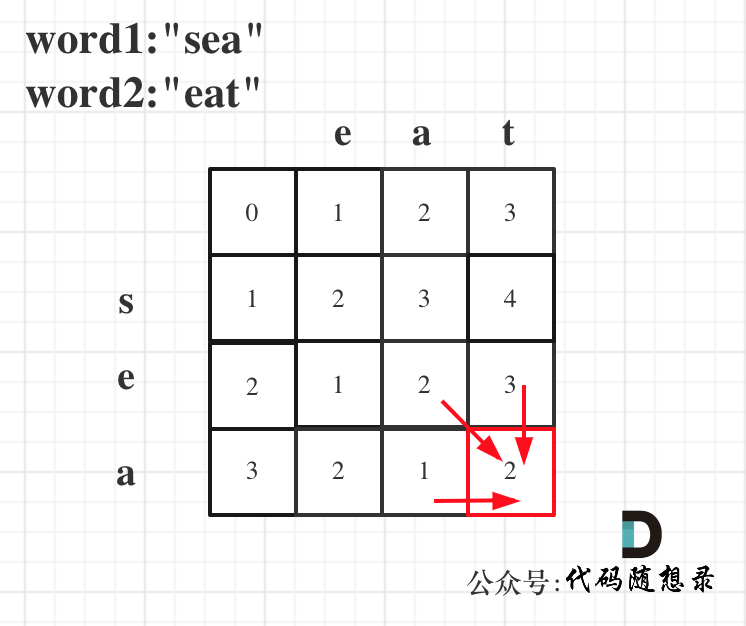
两个字符串的删除操作-583

这道题也是类公共子序列问题。设 dp[i][j] 表示 word1[i-1]、word2[j-1] 处所需的最小步数。

画一遍dp表，就有思路了： img.png

双循环遍历 word1、word2，有两种情况：
1、word1[i] == word2[j]; 此时不需要裁剪word1、word2，结果直接等于dp[i-1][j-1]。
2、word1[i] != word2[j]; 此时需要裁剪word1 或 word2。有两种裁剪方式：

第一种：裁剪word2，也就是在dp[i][j-1]，加多一步
第二种：裁剪word1，也就是在dp[i-1][j]，加多一步

Note: 在不理解，手画一遍dp 表，必懂。

临界条件：
1、当 word1 为 ""；
2、当 word2 为 ""；

得出转移方程：

\[dp[i][j] = \begin{cases} dp[i-1][j-1], & \text{if } word1[i-1] == word2[j-1] \\[6pt] min(dp[i-1][j], dp[i][j-1]), & \text{if } word1[i-1] != word2[j-1] \\[6pt] \end{cases}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

func minDistance(word1 string, word2 string) int {
	dp := make([][]int, len(word1)+1)
	for i := 0; i < len(word1)+1; i++ {
		dp[i] = make([]int, len(word2)+1)
		dp[i][0] = i

		if i == 0 {
			for j := 0; j < len(word2)+1; j++ {
				dp[i][j] = j
			}
		}
	}

	for i := 1; i < len(word1)+1; i++ {
		for j := 1; j < len(word2)+1; j++ {
			if word1[i-1] == word2[j-1] {
				dp[i][j] = dp[i-1][j-1]
			} else {
				dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + 1
			}
		}

	}

	return dp[len(word1)][len(word2)]
}

编辑距离-72

最终状态是 word1 与 word2 相等，八九不离十是子序列问题。

设 dp[i][j] 表示在 word1[i-1]、word2[j-1] 处，所需要最少操作数。

画出dp表，思路就清晰了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

      ""    r     o     s   
   +-----+-----+-----+-----+
"" |  0  |  1  |  2  |  3  |
   +-----+-----+-----+-----+
 h |  1  |  1  |  2  |  3  |
   +-----+-----+-----+-----+
 o |  2  |  2  |  1  |  2  |
   +-----+-----+-----+-----+
 r |  3  |  2  |  2  |  2  |
   +-----+-----+-----+-----+
 s |  4  |  3  |  3  |  2  |
   +-----+-----+-----+-----+
 e |  5  |  4  |  4  |  3  |
   +-----+-----+-----+-----+

遍历 word1 和 word2。有两种情况：
1、word1[i-1] == word2[j-1]；不需要任何操作，即：dp[i][j] == dp[i-1][j-1]
2、word1[i-1] != word2[j-1]；需要 1 步操作

  • word1 删除一个字符；即 dp[i][j] == dp[i-1][j] + 1；如上表 dp[3][2]
  • word2 删除一个字符；即 dp[i][j] == dp[i][j-1] + 1；如上表 dp[1][2]
  • word1、word2 增加相同的字符；即 dp[i][j] == dp[i-1][j-1] + 1；如上表 dp[3][3]

状态转移方程：

\[dp[i][j] = \begin{cases} dp[i-1][j-1], & \text{if } word1[i-1] == word2[j-1] \\[6pt] min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]), & \text{if } word1[i-1] != word2[j-1] \\[6pt] \end{cases}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

func minDistance(word1 string, word2 string) int {
	dp := make([][]int, len(word1) + 1)
	for i := 0; i < len(word1) + 1; i ++ {
		dp[i] = make([]int, len(word2) + 1)
		dp[i][0] = i
	}
	for j := 0 ;j < len(word2) + 1; j ++ {
		dp[0][j] = j
	}

	for i := 1 ; i <len(word1) + 1; i ++ {
		for j := 1; j <len(word2) + 1; j ++ {
			if word1[i-1] == word2[j-1] {
				dp[i][j] = dp[i-1][j-1]
			}else {
				dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1], dp[i-1][j])) + 1
			}
		}

		fmt.Print(dp[i])
	}

	return dp[len(word1)][len(word2)]
}

回文子串-647

根据回文字符串特点：对于一个字符串，如 cbabc，bab子串是回文数，s[0] 与 s[4] 相等，那么该字符串也是回文数。

动态规划讲究把问题拆分成子问题。

设 dp[start][end] 表示字符串 s[start: end] （左闭右闭）是否为回文数

为什么不能定义dp[start][end] 表示字符串中 回文子串 的数目?

答：核心是能不能拆分成子问题；根据回文子串特点，并不是依赖前 i-1 个子字符，而是依赖s[start-1: end-1]

s[start: end] 有2种情况：
1、s[start] != s[end]；那么这个子串不可能是回文子串
2、s[start] == s[end]；又分几种情况

  • 1 个字符；即start == end，那必须是回文子串
  • 2 个字符；即end - start == 1，那也是回文子串
  • 2 个字符以上；即end -start > 1，也是去掉头尾，还是一个回文子串，也就是 dp[start][end] = dp[start+1][end-1]
  • 其他场景都不是回文子串

根据以上分析，存在转移方程：dp[start][end] = dp[start+1][end-1]；所以dp 表的遍历顺序应该是从小到上，从左到右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

func countSubstrings(s string) int {
	if len(s) == 0 {
		return 0
	}

	dp := make([][]bool, len(s))
	for i := 0; i < len(s); i++ {
		dp[i] = make([]bool, len(s))
	}

	result := 0
	// start 从下到上
	for start := len(s) - 1; start >= 0; start-- {
		// end 从左到右
		for end := start; end < len(s); end++ {
			if s[start] != s[end] {
				continue
			}

			// 1个字符
			if start == end {
				dp[start][end] = true
				result++
			}
			// 2个字符
			if end-start == 1 {
				dp[start][end] = true
				result++
			}

			// 大于2个字符
			if end-start > 1 && dp[start+1][end-1] {
				dp[start][end] = true
				result++
			}
		}
	}

	return result
}

最长回文子序列-516

设 dp[start][end] 表示 s[start:end]（左闭右闭）最长回文子序列长度。

有以下几种情况：
1个字符；即 satrt == end，则 dp[start][end] == 1
2个字符；即 end - start = 1，

  • 当 s[start] != s[end]; dp[start][end] == 1
  • 当 s[start] == s[end]; dp[start][end] == 2
    大于2个字符；即 end - start > 1
  • 当 s[start] == s[end]; s[start]、s[end] 追加到字符s[start + 1][end - 1]会产生更长的回文子序列，则 dp[start][end] = dp[start + 1][end - 1] + 1
  • 当 s[start] != s[end]; 需要对比s[start] 或 s[end] 追加到字符s[start + 1][end - 1]哪种情况产生的回文子序列长度最大，则 dp[start][end] = max(dp[start+1][end], dp[start][end -1])

通过以上分析，dp[start][end] 依赖 dp[start + 1][end-1]、dp[start + 1][end]、dp[start][end - 1]，得出dp表的填充顺序是：从下到上，从左到右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

func longestPalindromeSubseq(s string) int {
	if len(s) == 0 {
		return 0
	}

	dp := make([][]int, len(s))
	for i := range dp {
		dp[i] = make([]int, len(s))
	}

	for start := len(s) - 1; start >= 0; start-- {
		for end := start; end < len(s); end++ {
			// 一个字符
			if start == end {
				dp[start][end] = 1
			}

			// 2个字符
			if end-start == 1 {
				if s[start] == s[end] {
					dp[start][end] = 2
				} else {
					dp[start][end] = 1
				}
			}

			// 大于2个字符
			if end-start > 1 {
				if s[start] == s[end] {
					dp[start][end] = dp[start+1][end-1] + 2
				} else {
					dp[start][end] = max(dp[start+1][end], dp[start][end -1])
				}
			}
		}
	}

	return dp[0][len(s)-1]
}
algorithm, dynamic-programming
algorithm dynamic programming
This post is licensed under CC BY 4.0 by the author.